Question

Suppose Z denotes the set of all integers, Z denotes the set of all positive integers, and Z− denotes the set of all negative integers. Similarly R denotes the set of all real numbers, R denotes the set of all positive real numbers, and R− denotes the set of all negative real numbers. Suppose N denotes the set of all natural numbers and Q denotes the set of all rational numbers. Enter "T" for each true, and "F" for each false statements.(a) Z / Q = Z(b) Z / Z- = N

Answer 1

a) False

b) False

Explanation:

We are given the following information:

Z is a set of all integers,
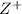`Z^+` is a set of all positive integers and
`Z^-` is a set of all negative integers.

Q is a set of all rational numbers,
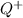`Q^+` is a set of all positive rational numbers and
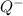`Q^-` is a set of all negative rational numbers.

N is a set of all natural numbers.

a) False

We will show this with the help of a counter example.

`Z = 3\\Q = (3)/(4)\\\displaystyle(Z)/(Q) = \displaystyle(3)/((3)/(4)) = \displaystyle(8)/(3)`

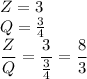
which is a rational number and not an integer.

b) False

We will show this with the help of a counter example.

`Z = 3\\Z^- = -5\\\displaystyle(Z)/(Z^-) = \displaystyle(3)/(-5) = -\displaystyle(3)/(5)`

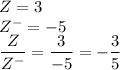
which is a rational number and not a natural number.