Question

23. In an attempt to escape his island, Gilligan builds a raft and sets to sea. The wind shifts a great deal during the day, and he is blown along the following straight lines: 2.50 km 45.0º north of west; then 4.70 km 60.0º south of east; then 1.30km 25.0º south of west; then 5.10 km straight east; then 1.70km 5.00º east of north; then 7.20 km 55.0º south of west; and finally 2.80 km 10.0º north of east. What is his final position relative to the island?

Answer 1

R=7.34km ∠ 63.47° South of East.

Step-by-step explanation:

We can either solve this graphically or by using the components of the given vectors. I'll solve it by using the components. So first we need to do a sketch of what the displacements will look like (See attached picture).

The piture is not drawn to scale, but it should help us visualize the directions better. I will name each displacement a different letter so we can distinguish them. We will say that if he goes north, he will have positive y-displacement, if he goes south, he will have negative y-displacement, if he goes east, he will have positive x-displacement and if he goes west, he will have negative x-displacement.

So having said this let's begin. So let's take the first displacement, displacement A:

2.50 km 45° north of west.

He goes north here which means he has positive y-displacement and he goes west, which means he has negative x-displacement. Its components can be found by using the sin and cos functions, like this:

`A_(x)=Acos(\theta)`

`A_(x)=2.50 cos (45^(o))`

`A_(x)=-1.7678km i`

`A_(y)=Asin(\theta)`

`A_(y)=2.50 sin (45^(o))`

`A_(y)=1.7678km j`

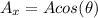
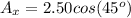
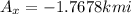
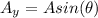
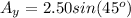
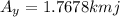
and we do the same with the other vectors.

B = 4.70km 60.0° south of east:

`B_(x)=2.35i km`

`B_(y)=-4.070j km`

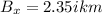
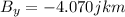
C = 1.30km 25.0° south of west:

`C_(x)=-1.1782i km`

`C_(y)=-0.549j km`

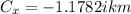
D = 5.10km straight east:

`D_(x)=5.10i km`

`D_(y)=0j km`

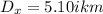
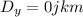
E = 1.70km 5.00° east of north

In this case we need to flip the functions due to the direction of the displacement.

`E_(x)=Esin(\theta)`

`E_(x)=1.70 sin (5^(o))`

`E_(x)=0.1482km i`

`E_(y)=Ecos(\theta)`

`E_(y)=1.70 cos (5^(o))`

`E_(y)=1.6935km j`

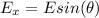
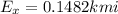
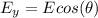
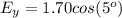
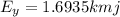
F = 7.20km 55.0° south of west:

`F_(x)=-4.13i km`

`F_(y)=-5.898j km`

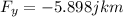
G = 2.80km 10.0° north of east:

`G_(x)=2.757i km`

`G_(y)=0.486j km`

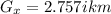
So now it's time to find the resulting vector, so we get:

`R_(x)=A_(x)+B_(x)+C_(x)+D_(x)+E_(x)+F_(x)+G_(x)`

`R_(x)=-1.7678i+2.35i-1.1782i+5.10i+0.1482i-4.13i+2.757i`

`R_(x)=3.2792i km`

`R_(y)=A_(y)+B_(y)+C_(y)+D_(y)+E_(y)+F_(y)+G_(y)`

`R_(y)=1.7678j-4.070j-0.549j+0j+1.6935j-5.898j+0.486j`

`R_(y)=-6.5697j km`

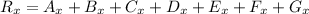
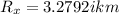
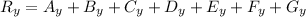
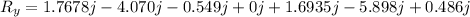
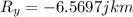
So, now that we have the components of the resultant vector we can find magnitude of the displacement and the angle.

`|R|=\sqrt {(3.2792)^(2)+(-6.5697)^(2)}`

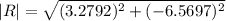
which yields

|R|=7.34 km

∠ =
`tan^(-1)((-6.5697)/(3.2792))`

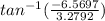
∠ = -63.47°

So the final position relative to the island is:

7.34km 63.47° South of east