Question

The probability that a lab specimen contains high levels of contamination is 0.10. A group of 4 independent samples are checked. Round your answers to four decimal places (e.g. 98.7654). (a) What is the probability that none contain high levels of contamination? (b) What is the probability that exactly one contains high levels of contamination? (c) What is the probability that at least one contains high levels of contamination?

Answer 1

a) 0.6561

b) 0.2916

c) 0.3439

Explanation:

We are given the following information:

Let us treat high level of contamination as our success.

p = P(High level of contamination) = P(success) = 0.10

n = 4

The, by binomial distribution:

`P(X=x) = \binom{n}{x}.p^x.(1-p)^(n-x)\\\text{where x is the number of success}`

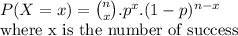
a) P(No high level of contamination)

We put x = 0, in the formula.

`P(X=0) = \binom{4}{0}.(0.10)^0.(1-0.10)^(4) =0.6561`

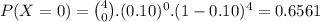
Probability that no lab specimen contain high level of contamination is 0.6561

b) P(Exactly one high level of contamination)

We put x = 1, in the formula.

`P(X=1) = \binom{4}{1}.(0.10)^1.(1-0.10)^(3) =0.2916`

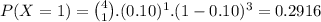
Probability that no lab specimen contain high level of contamination is 0.6561

c) P(At least one contains high level of contamination)

`p(x \geq 1) = 1 - p( x = 0) = 1 - 0.6561 = 0.3439`

Probability that at least 1 lab specimen contain high level of contamination is 0.3439