Question

Consider the midterm and final for a statistics class Suppose 10% students earned an A on the midterm. Of those students who earned an A on the midterm, 55% received an A on the final, and 15% of the students who earned lower than an A on the midterm received an A on the final. You randomly pick up a final exam and notice the student received an A. What is the probability that this student earned an A on the midterm?

Answer 1

There is a 29% probability that this student earned an A on the midterm.

Explanation:

The first step is that we have to find the percentage of students who got an A on the final exam.

Suppose 10% students earned an A on the midterm. Of those students who earned an A on the midterm, 55% received an A on the final, and 15% of the students who earned lower than an A on the midterm received an A on the final.

This means that

Of the 10% of students who earned an A on the midterm, 55% received an A on the final. Also, of the 90% who did not earn an A on the midterm, 15% received an A on the final.

So, the percentage of students who got an A on the final exam is

`P_(A) = 0.10(0.55) + 0.90(0.15) = 0.19`

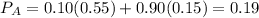
To find the probability that this student earned an A on the final test also earned on the midterm, we divide the percentage of students who got an A on both tests by the percentage of students who got an A on both tests.

The percentage of students who got an A on both tests is:

`P_(AA) = 0.10(0.55) = 0.055`

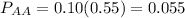
The probability that the student also earned an A on the midterm is

`P = (P_(AA))/(P_(A)) = (0.055)/(0.19) = 0.29`

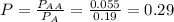
There is a 29% probability that this student earned an A on the midterm.