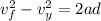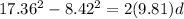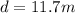Answer:
Part a)
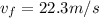
Part b)
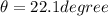
Part c)
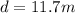
Step-by-step explanation:
Velocity just before it strike the ground is given as
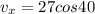
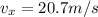
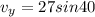

since there is no friction in horizontal direction so its speed in horizontal direction will remain same
Part a)
velocity in X direction
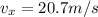
time taken by the skier to reach the ground is given as
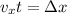
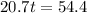
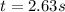
now in the same time it will cover vertical distance

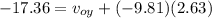
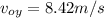
so magnitude of initial speed is given as
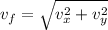
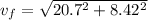
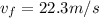
Part b)
Direction of velocity
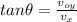
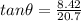
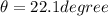
Part c)
Now in order to find the height of the ramp we can find the vertical displacement