Question

A 63.2-kg climber finds herself dangling over the edge of a cliff. Fortunately, she’s connected by a rope of negligible mass to a 1220-kg rock located 48.6 m from the edge of the cliff. Unfortunately, the ice is frictionless, so the climber accelerates downward. What’s her acceleration, and how much time does she have before the rock goes over the edge?

Answer 1

Answer:
`0.535 m/s^2`

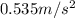
Step-by-step explanation:

Given

mass of climber
`(m_1)=63.2 kg`

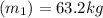
Distance between rock and cliff=48.6 m

mass of rock
`(m_2)=1220`

let T be the tension in the rope

Thus
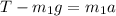`T-m_1g=m_1a`------1

where a is the acceleration of system

Also for Rock

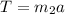`T=m_2a`------2

From 1 & 2 we can say that

`m_1\left [ g+a\right ]=m_2\left [ a\right ]`

`g+a=(1220)/(63.2)\left [ a\right ]`

g+a=19.303 a

g=18.303 a

`a=(g)/(18.303)`

`a=0.535 m/s^2`

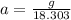
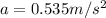
Thus climber is decelerating with
`0.535 m/s^2`

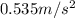
time to cover 48.6 m

`48.6=(0.535t^2)/(2)`

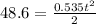
t=13.47 s