Answer:
Velocity,v = 0.323 m/s
Step-by-step explanation:
The acceleration of a particle is given by :
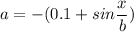
b = 0.8 m when x = 0
Since,

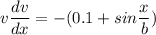
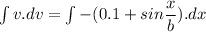
![(v^2)/(2)=-[0.1x-0.8cos(x)/(0.8)]+c](https://img.qammunity.org/2020/formulas/physics/college/gd3uuqbvpoealyn7gxoth9ycbgdm04gx05.png)
At x = 0, v = 1 m/s
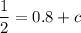

![(v^2)/(2)=-[0.1x-0.8cos(x)/(0.8)]-0.3](https://img.qammunity.org/2020/formulas/physics/college/w5gqbctr10x50yiikf4t1afvw7zwlj7n1k.png)
At x = -1 m
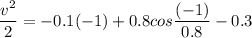

v = 0.323 m/s
So, the velocity of the particle is 0.323 m/s. Hence, this is the required solution.