Answer:
60.9 g
Step-by-step explanation:
The formula for the calculation of moles is shown below:
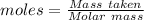
Given: For
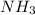
Given mass = 90.1 g
Molar mass of
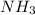 = 17.031 g/mol
= 17.031 g/mol
Moles of
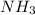 = 90.1 g / 17.031 g/mol = 5.2904 moles
= 90.1 g / 17.031 g/mol = 5.2904 moles
Given: For

Given mass = 90.1 g
Molar mass of
 = 31.9988 g/mol
= 31.9988 g/mol
Moles of
 = 90.1 g / 31.9988 g/mol = 2.8157 moles
= 90.1 g / 31.9988 g/mol = 2.8157 moles
According to the given reaction:
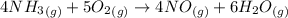
4 moles of
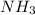 react with 5 moles of
react with 5 moles of

1 mole of of
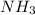 react with 5/4 moles of
react with 5/4 moles of

5.2904 moles of
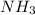 react with
react with
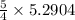 mole of
mole of

Moles of
 = 6.613 moles
= 6.613 moles
Available moles of
 = 2.8157 moles
= 2.8157 moles
Limiting reagent is the one which is present in small amount. Thus,
 is limiting reagent. (2.8157 < 6.613)
is limiting reagent. (2.8157 < 6.613)
The formation of the product is governed by the limiting reagent. So,
5 moles of
 gives 6 moles of
gives 6 moles of
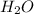
1 mole of
 gives 6/5 moles of
gives 6/5 moles of
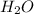
2.8157 moles of
 gives
gives
 moles of
moles of
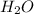
Moles of water = 3.37884 moles
Molar mass of
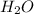 = 18.0153 g/mol
= 18.0153 g/mol
Mass of
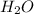 = Moles × Molar mass = 3.37884 × 18.0153 g = 60.9 g
= Moles × Molar mass = 3.37884 × 18.0153 g = 60.9 g