Question

Radioactive decay can be described by the following equation where is the original amount of the substance, is the amount of the substance remaining after time , and is a constant that is characteristic of the substance. For the radioactive isotope iron-55, is If the original amount of iron-55 in a sample is 32.2 mg, how much iron-55 remains after 2.41 years have passed? mg

Answer 1

Iron remains = 17.49 mg

Step-by-step explanation:

Half life of iron -55 = 2.737 years (Source)

`t_(1/2)=\frac {ln\ 2}{k}`

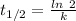
Where, k is rate constant

So,

`k=\frac {ln\ 2}{t_(1/2)}`

`k=\frac {ln\ 2}{2.737}\ year^(-1)`

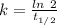
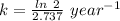
The rate constant, k = 0.2533 year⁻¹

Time = 2.41 years

`[A_0]` = 32.2 mg

Using integrated rate law for first order kinetics as:

`[A_t]=[A_0]e^(-kt)`

Where,

`[A_t]` is the concentration at time t

`[A_0]` is the initial concentration

So,

`[A_t]=32.2* e^(-0.2533* 2.41)\ mg`

`[A_t]=32.2* e^(-0.610453)\ mg`

`[A_t]=17.49\ mg`

Iron remains = 17.49 mg