Answer:
Part a)
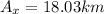
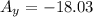

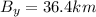
Part b)
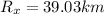
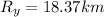
Part c)
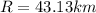
 North of East
North of East
Step-by-step explanation:
Part a)
Hiker's displacement on first day of the motion is given as
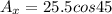
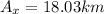
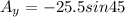

His displacement on second day



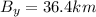
Part b)
Now hiker's net displacement along East
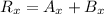

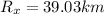
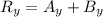
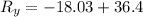
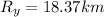
Part c)
Magnitude of net displacement is given as
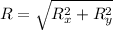
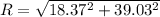
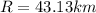
direction of the net displacement is given as
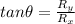
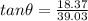
 North of East
North of East