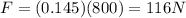Question

The acceleration of a baseball pitcher's hand as he delivers a pitch is extreme. For a professional player, this acceleration phase lasts only 50 ms, during which the ball's speed increases from 0 to about 90 mph, or 40 m/s.

Answer 1

116 N

Step-by-step explanation:

Missing question: (found on google)

"What is the force of the pitcher's hand on the 0.145 kg ball during this acceleration phase?

Express your answer with the appropriate units."

Solution:

First of all, we need to calculate the acceleration of the ball, given by

`a=(v-u)/(\Delta t)`

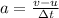
where

v = 40 m/s is the final velocity

u = 0 is the initial velocity

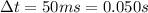`\Delta t = 50 ms = 0.050 s` is the duration of the acceleration phase

Substituting,

`a=(40-0)/(0.05)=800 m/s^2`

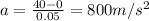
Now we can find the force exerted on the ball by using Newton's second law:

`F=ma`

where

m = 0.145 kg is the mass of the ball

a is the acceleration

Substituting,

`F=(0.145)(800)=116 N`