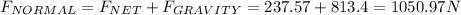Answer:
(A) Time period T = 6.28 SEC
(B) At highest point fore is - 575.83 N
(B) At lowest point force is 1050.97 N
Step-by-step explanation:
We have given that mass m = 83 kg
Radius r = 13 m
Speed v = 6.10 m/sec
(A) Time period of the motion is given by
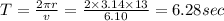
(b) Net force is given by
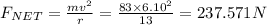
Force due to gravity
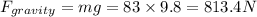
At highest point
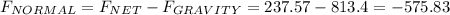
(B) At lowest point