Question

The "feasible region" has vertices (4,5), (4,6), (7,4), and (3,6). If the "objective function" that you are trying to minimize is C = 4x + 2y, what is the minimum value? Write the minimum value, not the point.

Answer 1

The minimum value is 24

Explanation:

we know that

The "feasible region" has vertices
`(4,5), (4,6), (7,4),(3,6)`

The objective function is
`C=4x+2y`

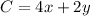
To determine the minimum value of the objective function, substitute the value of x and the value of y of each vertex in the objective function and then compare the values

1) For (4,5)

x=4,y=5

`C=4(4)+2(5)=26`

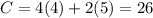
2) For (4,6)

x=4,y=6

`C=4(4)+2(6)=28`

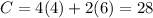
3) For (7,4)

x=7,y=4

`C=4(7)+2(4)=36`

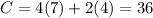
4) For (3,6)

x=3,y=6

`C=4(3)+2(6)=24`

therefore

The minimum value is 24