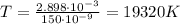Question

What is the temperature of a star (in Kelvin) if its peak wavelength is 150 nm (that is, 150 x 10^-9 m)?

Answer 1

19320 K

Step-by-step explanation:

The temperature of a star is related to its peak wavelength by Wien's displacement law:

`T=(b)/(\lambda)`

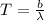
where

T is the absolute temperature at the star's surface

`b=2.898 \cdot 10^(-3)m\cdot K` is Wien's displacement constant

`\lambda` is the peak wavelength

Here we have

`\lambda=150 nm = 150\cdot 10^(-9)nm`

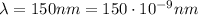
Substituting into the equation, we find

`T=(2.898\cdot 10^(-3))/(150\cdot 10^(-9))=19320 K`