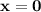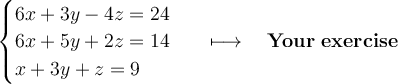
Reorder
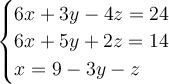
Substitute one of the equations:
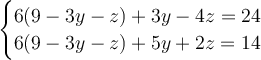
Apply the multiplicative law of distribution.
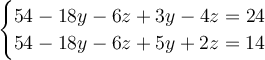
Combine as terms.
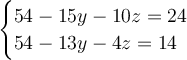
Rearrange the unknown terms on the left side of the equation.
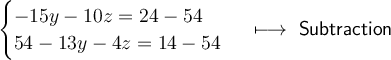
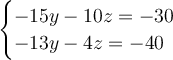
Rearrange like terms on the same side of the equation.
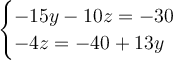
Divide both sides of the equation by the coefficient of the variable.
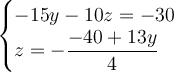
Substitute for one of the equations.
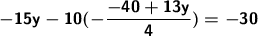
Reduce the expression to the least term.
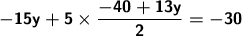
Multiply both sides by the common denominator.
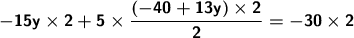
Simplify the fractions.
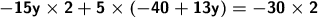
Aplicar la ley multiplicativa de distribución.
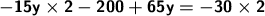
Multiply the monomial.
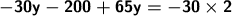
Calculate the product or coefficient.
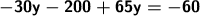
Combine as terms.
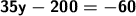
Rearrange the unknown terms on the left side of the equation.
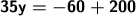
Calculate the sum or difference.
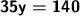
Divide both sides of the equation by the coefficient of the variable.
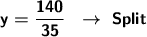
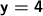
Substitute for one of the equations.
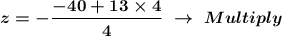
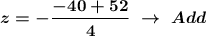
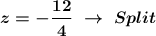
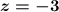
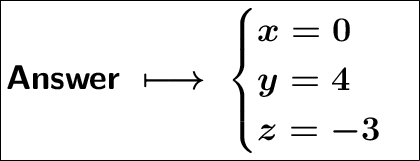
The system solution is:
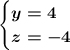
Substitute for one of the equations.
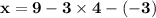
Calculate