Answer:
The height of the tower nearby the pole is 102 m.
Solution:
Given,
Height of the pole = 3.5 m
Length of the shadow of the pole = 1.47 m
Length of the shadow of the tower nearby = 42.75 m
Let us assume the height of the tower as x
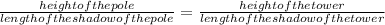
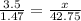
On solving for x we get,
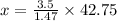

On rounding off to the nearest meter we get,
x=102 m
 The height of the tower is 102 meter.
The height of the tower is 102 meter.