Answer:
40 miles to his destination.
Explanation:
If the distance to the destination is a linear function of his driving time then the function f(x) has the form f(x)=mx + b
Now we're going to write two equations with the data that was given to us to find the function for this problem:

Therefore the equation f(x), is f(x) = -0.75x+103.75
To find how many miles he will have after driving 85 minutes:
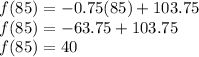
He will have 40 miles to his destination