Answer:
The required inequality is:
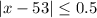
The least and the greatest percent of people that think their team will win the state championship is 52.5% and 53.5% respectively.
Explanation:
Consider the provided information.
In a sports poll, 53% of those surveyed believe their high school football team will win the state championship.
The poll shows a margin of error of 0.5 percentage points.
Let x is the actual number of percent of people that think their team will win the state championship.
The absolute difference of x and 53 should be less than or equal to 0.5
Therefore, the required inequality is:
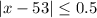
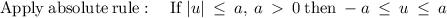
By using the above rule we can solve the inequality as shown:

Add 53 as shown:
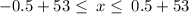
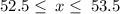
Hence, the least and the greatest percent of people that think their team will win the state championship is 52.5% and 53.5% respectively.