Answer:
a) 0.658 seconds
b) 0.96 inches
Step-by-step explanation:
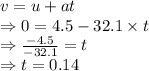
Time taken by the ball to reach the highest point is 0.14 seconds
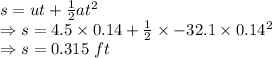
The highest point reached by the snowball above its release point is 0.315 ft
Total height the snowball will fall is 4+0.315 = 4.315 ft
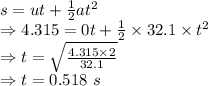
The snowball will reach the bank at 0.14+0.518 = 0.658 seconds after it has been thrown
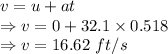
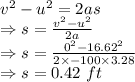
The snowball goes 0.5-0.42 = 0.08 ft = 0.96 inches