Question

For a fishing tournament the minimum length of a snook is 32 inches. The maximum length is 36 inches. Write and solve an absolute value equation that has these minimum and maximum lengths as it’s solutions.

Answer 1

|x - 34| = 2

Explanation:

In order to find an absolute value equation that has the given solutions, let x represent the lenght for the given problem

So, the solutions are: x=32 and x=36

You have to calculate the midpoint of x=32 and x=36 because the absolute value from any of the given solutions to the midpoint is the same (the distance is the same)

The midpoint is:

`(36+32)/(2) = 34`

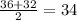
The distance from x=36 and the midpoint 34 can be calculated as:

36-34=2, which is the same distance from x=32 to the midpoint

So, x differ from the midpoint by 2 units

In conclussion, the absolute value of the difference between x and the midpoint equals 2:

|x - 34| = 2

Therefore, you have to solve the equation and prove that x=32 and x=36 are the solutions

Solving the equation:

By definition of absolute value, the expression between the absolute value is set to ± the number on the other side of the equality

x-34=2 (I) and x-34= -2 (II)

The solution of (I) is:

x=2+34

Therefore x=36

The solution of (II) is:

x=-2+34

Therefore x=32