Question

Tickets at a particular movie theater have different rates for adults and children. On Monday, the theater sold 8 adult tickets and 2 child tickets for $122. The next day, the theater sold 5 adult tickets and 9 children tickets for $115. What is the price for the child ticket?

Answer 1

Price for the child ticket (y) is 5 dollars.

Explanation:

Let the price of adult tickets be x and price of child tickets be y.

Since theater sold 8 adult ticket and 2 child tickets for $122, therefore

Price of 8 adult tickets = 8x

Price of 2 child tickets = 2y

According to question,

8x + 2y = 122 ............(1)

8x = 122 -2y

`x = (122 - 2y)/(8)`

`x = (61 - y)/(4)`

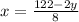
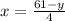
Similarly, Price of 5 adult tickets = 5x

Price of 9 child tickets = 9y

According to question,

5x + 9y = 115

By substituting the value of x

=
`5((61 - y)/(4)) + 9y = 115`

=
`305 - 5y + 4 (9y) = 115 * 4`

=
`- 5y + 36 y = 460 - 305`

=
`31 y = 155`

=
`y = (155)/(31) = 5\ dollars`

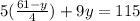
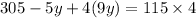
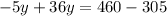
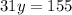
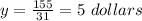
Therefore the price for the child ticket is 5 dollars.