Answer: The probability that no requests for assistance are in the system is 0.1667.
Explanation:
Since we have given that
Arrival rate =
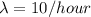
Service rate =
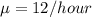
the probability that no requests for assistance are in the system is given by
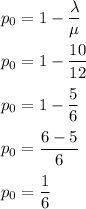
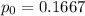
Hence, the probability that no requests for assistance are in the system is 0.1667.