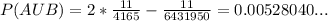Question

A bridge hand (thirteen cards) is dealt from a standard fifty-two-card deck. Let A be the event that the hand contains four aces; let B be the event that the hand contains four kings. Find P(A ∪ B). Larsen, Richard J.. An Introduction to Mathematical Statistics and Its Applications (p. 98). Pearson Education. Kindle Edition.

Answer 1

The probability that the hand contains four kings or four aces is given by P(A ∪ B) = 0.00528040... or approximately 0.528%.

Explanation:

This is a combinatory rule problem in which, for every n attempts you get p successes, its denoted nCp. In terms of a bridge hand this means that if you have n number of possible cards, you choose p of them.

The number of possible combinations is given by:

`nCp=\left(\begin{array}{c}n&p\end{array}\right)=(n!)/(p!(n-p!))`

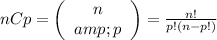
The probability of event A and event B are the same since every one of them involves getting 4 cards of the same suit.

P(A)=P(B)

For the problem, you can have the aces in 4C4 ways, and the remaining 9 cards in 48C9 ways. The number of different bridges hands that a 52 cards deck can have is 52C13. Then you can solve P(A):

`P(A)=\left(\begin{array}{c}4&4\end{array}\right)\left(\begin{array}{c}48&9\end{array}\right)/\left(\begin{array}{c}52&13\end{array}\right)`

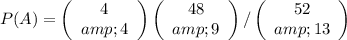
Using the definition of combinatory rule you can solve the factorial operations:

`P(A)=P(B)=(11)/(4165)`

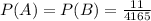
Then you have that P(A∪B)=P(A)+P(B)-P(A∩B)

P(A∩B is the event that the bridge has 4 aces and 4 kings.

P(A∩B)=
`\left(\begin{array}{c}8&8\end{array}\right)\left(\begin{array}{c}44&5\end{array}\right)/\left(\begin{array}{c}52&13\end{array}\right)`

`P(A)=P(B)=(11)/(6431950)`

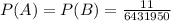
Then you can solve P(AUB)=

`P(AUB)=2*(11)/(4165)-(11)/(6431950)=0.00528040...`