Question

You whirl a ball tied to a light string of negligible mass in a vertical circle in the clockwise direction. The mass of the ball is 0.200 kg and the length of the string is 0.660 m. You maintain the center of the circle to be at a constant height of 2.80 m from the floor. If the string breaks when the ball is at the lowest point and its speed is 2.50 m/s, where on the floor does it land? Express your answer in vector form with the center of the circle as the origin.

Answer 1

d= - 1.63 i - 2.14 j

Step-by-step explanation:

Given that

m= 0.2 kg

r = 0.66 m

H = 2.8 m

Height from ground ,h=2.8 - 0.66

h=2.14 m/s

u= 2.5 m/s

When the string breaks then ball have only horizontal direction and velocity in vertical direction(v) is zero.

The time taken by ball to strike the floor

`h=v.t+(1)/(2)gt^2`

`2.14=(1)/(2)* 10* t^2`

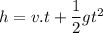
t= 0.65 sec

So the distance cover in horizontal direction ,x

x = u .t

x = 2.5 x 0.65

x=1.63 m

y= =2.14

So in the vector form

d= - 1.63 i - 2.14 j