Answer:
Explanation:
If you want to determine the domain and range of this analytically, you first need to factor the numerator and denominator to see if there is a common factor that can be reduced away. If there is, this affects the domain. The domain are the values in the denominator that the function covers as far as the x-values go. If we factor both the numerator and denominator, we get this:
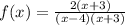
Since there is a common factor in the numerator and the denominator, (x + 3), we can reduce those away. That type of discontinuity is called a removeable discontinuity and creates a hole in the graph at that value of x. The other factor, (x - 4), does not cancel out. This is called a vertical asymptote and affects the domain of the function. Since the denominator of a rational function (or any fraction, for that matter!) can't EVER equal 0, we see that the denominator of this function goes to 0 where x = 4. That means that the function has to split at that x-value. It comes in from the left, from negative infinity and goes down to negative infinity at x = 4. Then the graph picks up again to the right of x = 4 and comes from positive infinity and goes to positive infinity. The domain is:
(-∞, 4) U (4, ∞)
The range is (-∞, ∞)
If you're having trouble following the wording, refer to the graph of the function on your calculator and it should become apparent.