Answer:
Wavelength,
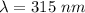
Step-by-step explanation:
It is given that,
Energy in most stable state,
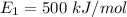
Energy in its lowest excited state,

Let
 is the wavelength of the radiation emitted when an atom of X undergoes a transition from the lowest excited state to the ground state. It can be calculated as :
is the wavelength of the radiation emitted when an atom of X undergoes a transition from the lowest excited state to the ground state. It can be calculated as :
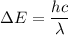
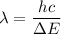
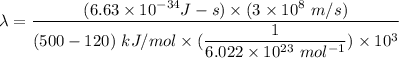
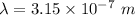
or
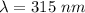
So, the wavelength of the radiation emitted when an atom of X undergoes a transition from the lowest excited state to the ground state is 315 nm. Hence, this is the required solution.