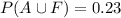Answer: 0.23
Explanation:
Given : F is the event "works in the finishing department;"
and A is the event "is absent excessively."
Given : 10% of all plant employees work in the finishing department; 20% of all plant employees are absent excessively; and 7% of all plant employees work in the finishing department and are absent excessively.
i.e. P(A)= 0.20 ; P(F)=0.10 ; P(A ∩ F) = 0.07
We know that

Then,
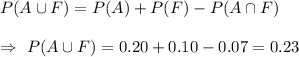
Hence, the required answer is