Answer:
Additional time of 1.91 seconds is required before the ball passes the tree branch on the way back down.
Explanation:
Consider upward direction as positive,
Here we need to find time interval between first and second 7 m displacements.
We have equation of motion, s = ut + 0.5 at²
Displacement, s = 7 m
Initial velocity, u = 15 m/s
Acceleration, a = -9.81 m/s²
Substituting
s = ut + 0.5 at²
7 = 15 t + 0.5 x -9.81 x t²
4.905 t² - 15 t + 7 = 0
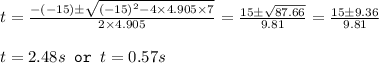
So at t = 0.57 s and t = 2.48 s the displacement is 7 m
Interval between them = 2.48 - 0.57 = 1.91 s
So additional time of 1.91 seconds is required before the ball passes the tree branch on the way back down.