Answer:
mass of the other asteroid =

Step-by-step explanation:
We use the definition for the force between two celestial objects under the action of the gravity they produce using newton's general gravitational constant:
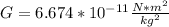
The force between the two asteroids will then be given by:
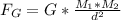
where G is Newton's gravitational constant, the asterioid's masses are M1 and M2 respectively, and d is the distance between them.
We replace the known values in he equation above, and solve for the missing mass:
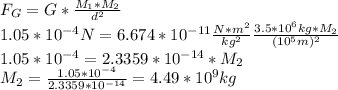
Since the units for the given quantities are all in the SI system, our resultant units for the unknown mass of the asteroid will be in kg.