Answer:
The center, vertices and foci of the ellipse with equation
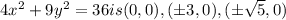 respectively
respectively
Solution:
The equation of ellipse with centre (0, 0) in the form of
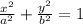 --- eqn 1
--- eqn 1
Where,
x is the major axis
Centre (0, 0)
Vertices is

Foci is
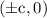 where
where
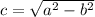
Now given that the equation of ellipse is
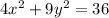 --- eqn 2
--- eqn 2
On dividing equation (2) by 36,
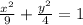
On comparing equations (1) and (2),
We get a = 3, b= 2
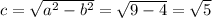
So centre of
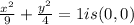
Vertices of
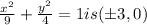
Foci of
