Answer:
95.994% , or about 96%
Explanation:
Complete Question:
When professional golfer Jordan Spieth hits his driver, the distance the ball travels can be modeled by a Normal Distribution with Mean = 304 yards and Standard Deviation = 8 yards.
a) On a specific hole, Jordan would need to hit the ball at least 290 yards to have a clear second shot that avoids a large group of trees. What percent of Spieth's drives travel at least 290 yards?
Solution:
We want to find % of drives that go more than 290 yards. The parameters of Normal Distribution are mean and standard deviation (given). Thus:
N(304,8)
Now,
We need z score, that has formula:

Where mu is mean and sigma is standard deviation
Now, we have:
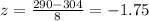
If we look at z-table, we can figure out the corresponding value (area) to be 0.95994
Thus we can say 95.994% or about 96% of Spieth's drives travel more than 290 yards.