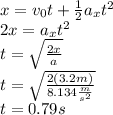Question

To meet a U.S. Postal Service requirement, employees' footwear must have a coefficient of static friction of 0.5 or more on a specified tile surface. A typical athletic shoe has a coefficient of 0.830. In an emergency, what is the minimum time interval in which a person starting from rest can move 3.20 m on a tile surface if she is wearing the following footwear?

Answer 1

0.79 s

Step-by-step explanation:

We have to calculate the employee acceleration, in order to know the minimum time. According to Newton's second law:

`\sum F_x:f_(max)=ma_x\\\sum F_y:N-mg=0`

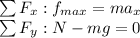
The frictional force is maximum since the employee has to apply a maximum force to spend the minimum time. In y axis the employee's acceleration is zero, so the net force is zero. Recall that
`f_(max)=\mu N`

Now, we find the acceleration:

`\mu N=ma_x\\\mu mg=ma_x\\a_x=\mu g\\a_x=0.83(9.8(m)/(s^2))\\a_x=8.134(m)/(s^2)`

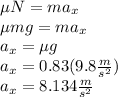
Finally, using an uniformly accelerated motion formula, we can calculate the minimum time. The employee starts at rest, thus his initial speed is zero:

`x=v_0t+(1)/(2)a_xt^2\\2x=a_xt^2\\t=\sqrt{(2x)/(a)}\\t=\sqrt{(2(3.2m))/(8.134(m)/(s^2))}\\t=0.79 s`