Question

A satellite system consists of n components and functions on any given day if at least k of the n components function on that day. On a rainy day, each of the components independently functions with probability p1, whereas on a dry day, each independently functions with probability p2. If the probability of rain tomorrow is α, what is the probability that the satellite system will function?

Answer 1

P = αP(x≥k,p1) + (1-α)P(x≥k,p2)

Explanation:

The probability that k of n components function on a day follows a binomial distribution, so the probability is:

`P(k,p)=nCk*p^(k)*(1-p)^(n-k)`

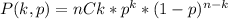
Where p is the probability that a component function and nCk is
`(n!)/(k!(n-k)!)`

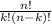
So, the probability that at least k of the n components function on a day is:

P(x≥k,p) = P(k,p) + P(k+1,p) + P(k+2,p) + ... + P(n,p)

Then, if it is rain, the probability of the function p is equal to p1, if it isn't the probability p is equal to p2, so the probability P that the satellite system will function is:

P = αP(x≥k,p1) + (1-α)P(x≥k,p2)

Where, P(x≥k,p1) and P(x≥k,p2) are equal to:

P(x≥k,p1) = P(k,p1) + P(k+1,p1) + P(k+2,p1) + ... + P(n,p1)

P(x≥k,p2) = P(k,p2) + P(k+1,p2) + P(k+2,p2) + ... + P(n,p2)