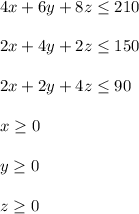Question

Q4. A fish processing company in Charlotteville processes three types of products: Type A,Type B and Type C.Its operations involve three basic activities: cleaning,cutting and packaging. Type A products require 4 minutes of cleaning 2 minutes of cutting and 2 minutes of packaging time.Type B products require 6 minutes of cleaning 4 minutes of cutting and 2 minutes of packaging time.Type C products require 8 minutes of cleaning 2 minutes of cutting and 4 minutes of packaging time. Given that the total time available for cleaning,cutting and packaging is 3.5hours,2.5 hours and 1.5 hours respectively. A. Clearly defining your variables,show the model which represents the information given in this problem.State any restrictions on the variables in the problem.

Answer 1

`4x+6y+8z\le 210\\ \\2x+4y+2z\le 150\\ \\2x+2y+4z\le 90\\ \\x\ge 0\\ \\y\ge 0\\ \\z\ge 0`

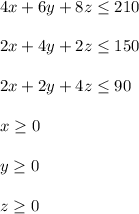
Explanation:

Let

• x the amount of type A produced;
• y the amount of type B produced;
• z the amount of type C produced.

Cleaning requires 4 minutes for type A, 6 minutes for type B and 8 minutes for type C. In total, 3.5 hours, then

`4x+6y+8z\le 3.5\cdot 60`

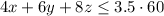
Cutting requires 2 minutes for type A, 4 minutes for type B and 2 minutes for type C. In total, 2.5 hours, then

`2x+4y+2z\le 2.5\cdot 60`

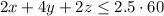
Packaging requires 2 minutes for type A, 2 minutes for type B and 4 minutes for type C. In total, 1.5 hours, then

`2x+2y+4z\le 1.5\cdot 60`

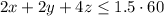
Note that

`x\ge 0\\y\ge 0\\z\ge 0`

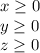
Hence, we have 6 inequalities:

`4x+6y+8z\le 210\\ \\2x+4y+2z\le 150\\ \\2x+2y+4z\le 90\\ \\x\ge 0\\ \\y\ge 0\\ \\z\ge 0`