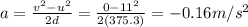Question

20 POINTS !

An engineer in a locomotive sees a car stuck
on the track at a railroad crossing in front of
the train. When the engineer first sees the
car, the locomotive is 380 m from the crossing
and its speed is 11 m/s.
If the engineer’s reaction time is 0.43 s,
what should be the magnitude of the minimum deceleration to avoid an accident?
Answer in units of m/s^2

Answer 1

`-0.16 m/s^2`

Step-by-step explanation:

First of all, we need to calculate the distance covered by the locomotive during the reaction time. This is given by

`d_1 = u t_1`

where

u = 11 m/s is the initial velocity of the locomotive

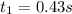`t_1=0.43 s` is the reaction time

Substituting,

`d_1 = (11)(0.43)=4.7 m`

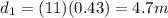
So the distance left between the locomotive and the car is

`d=380-4.7 =375.3 m`

Now we can find the minimum deceleration to avoid the accident with the equation

`v^2-u^2=2ad`

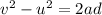
where

v = 0 is the final velocity

u = 11 m/s

a is the deceleration

d = 375.3 m is the stopping distance

Solving for a,

`a=(v^2-u^2)/(2d)=(0-11^2)/(2(375.3))=-0.16 m/s^2`