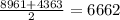Question

An insurance institute conducted tests with crashes of new cars traveling at 6 mi/h. The total cost of the damages was found for a simple random sample of the tested cars and listed below. Find the a)mean, b)median c) mode, d) midrange for the given sample data. Do the different measures of center differ very much?$7,431 $4,859 $8,961 $6,372 $4,363

Answer 1

Mean = $6,397.2

Median = $6,372

Midrange = $6,662

Explanation:

We are given the following data:

$7,431, $4,859, $8,961, $6,372, $4,363

Formula:

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Median:\\\text{If n is odd, then}\\\\Median = \displaystyle(n+1)/(2)th ~term \\\\\text{If n is even, then}\\\\Median = \displaystyle((n)/(2)th~term + ((n)/(2)+1)th~term)/(2)`

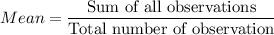
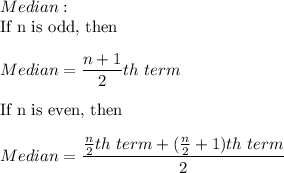
Mode is the most frequent observation in the dataset.

`Midrange = \displaystyle\frac{\text{Highest term} + \text{Lowest term}}{2}`

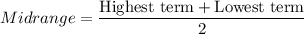
Mean =
`(31986)/(5) = 6397.2`

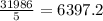
Median:

Data in increasing order: 4363, 4859, 6372, 7431, 8961

Median =
`3^(rd)\text{ term}` = 6372

Mode: All values appeared once.

Midrange =
`(8961+4363)/(2) = 6662`