Question

A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 20% salt and Solution B is 70% salt. She wants to obtain 110 ounces of a mixture that is 30% salt. How many ounces of each solution should she use?

Answer 1

88 ounces of 20% salt solution A must be mixed with 22 ounces of 70% salt solution B to obtain 110 ounces of 30% solution.

SOLUTION:

First, set up a table. fill in the unknowns with variables x and y. The table is attached below.

From the table, we can easily set up the two equations.

Sum of values of two salts = Value of mixture

0.2x+0.7y=33

For convenience, we'll multiply the entire equation by 10,

2 x + 7 y = 330 ------ eqn (1)

Now, Sum of amounts of each salt = Amount of mixture

x + y = 110 --------- eqn (2)

multiply eqn (2) with “2” for easy calculation and derive the equation into one variable.

2x + 2y = 220 --- eqn 3

Subtracting equation (3) from (1), we get

0 + 5y = 110

Thus, 5y = 110

`y = (110)/(5) = 22`

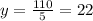
Substituting y = 22 in (2),

2x + 2(22) = 220

2x + 44 = 220

2 x = 220 - 44 = 176

`x = (176)/(2) = 88`

So, we have x = 88 and y = 22

We can conclude that 88 ounces of 20% salt solution A must be mixed with 22 ounces of 70% salt solution B to obtain 110 ounces of 30% solution.