Question

A rectangular swimming pool has a length of L yards and a width 5 yards less than its length. How much does it cost to border the outside

of the pool using 1-yard square tiles that cost $4 each?
A) (16L- 40) dollars
B) (16L - 24) dollars
C) (4L - 6) dollars
D) (16L - 20) dollars

Answer 1

A) (16L- 40) dollars

Explanation:

Givens

• The length of the pool is L yards.
• The width of the pool is 5 yards less than its length.

According to the given statements, length and width are related with

`W=L-5`

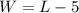
Then, we need to find the perimeter expression. Remember that the perimeter is the sum of all sides

`P=L+L+W+W\\P=2L+2W\\P=2(L+W)\\P=2(L+L-5)\\P=2(2L-5)`

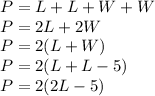
We know that each tile cost $4, and they cover all the perimeter. So, we multiply to find the total cost

`C=4P\\C=4(2(2L-5))\\C=16L-40`

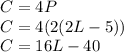
That is, the total cost is (16L - 40) dollars.

Therefore, the right answer is A.

Answer 2

A) (16L- 40) dollars

Explanation:

Given in the question that the dimensions of the pool are;

Length= L yards

Width= L-5 yards

Finding the perimeter of the pool

P=2(l+w) where l is length and w is width

P=2(L+L-5)

P=2(2L-5)

P=4L-10

The cost for 1 yard square tile is $4

The border will cost ;

$4(4l-10)

$ (16 l-40)