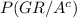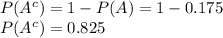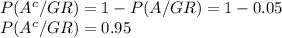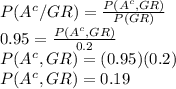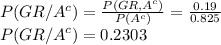Question

Suppose that an insurance company classifies people into one of three classes —good risks, average risks, and bad risks. Their records indicate that the probabilitiesthat good, average, and bad risk persons will be involved in an accident over a1-year span are, respectively, .05, .15, and .30.

a. If 20 percent of the populationare "good risks," 50 percent are "average risks," and 30 percent are "bad risks,"what proportion of people have accidents in a fixed year?
b. If policy holder A hadno accidents in 1987, what is the probability that he or she is a good (average)risk?

Answer 1

a. 17.5 %

b. 0.2303

Explanation:

Let's start defining the conditional probability :

Suppose two events A and B where
`P(A)>0` and
`P(B)>0`

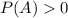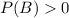
and P(A ∩ B) = P(A,B) where (A ∩ B) is the event where A and B occur both at the same time.

The conditional probability :

`P(A/B)=(P(A,B))/(P(B)) \\P(B/A)=(P(A,B))/(P(A))`

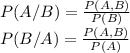
Let's define the following events :

A : ''Randomly chosen person had accident in a fixed year''

GR : ''The person belongs to good risks classification''

AR : ''The person belongs to average risks classification''

BR : ''The person belongs to bad risks classification''

The information given is :

`P(GR)=0.20\\P(AR)=0.50\\P(BR)=0.30`

`P(A/GR)=0.05\\P(A/AR)=0.15\\P(A/BR)=0.30`

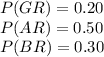
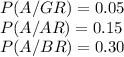
a.

We need to calculate
`P(A)`

`P(A)=P(A,GR)+P(A,AR)+P(A,BR)\\P(A)=P(A/GR).P(GR)+P(A/AR).P(AR)+P(A/BR).P(BR)\\P(A)=(0.05)(0.2)+(0.15)(0.5)+(0.30)(0.30)\\P(A)=0.175`

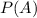
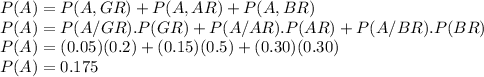
Then 17.5% of people have accidents in a fixed year

b. If U is an event ⇒

`P(U)=1-P(U^(c))`

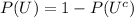
Where
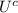`U^(c)` is the event where U does not occur

We need to calculate :

`P(GR/A^(c))`

`P(A^(c))=1-P(A)=1-0.175\\P(A^(c))=0.825`

`P(A^(c)/GR)=1-P(A/GR)=1-0.05\\P(A^(c)/GR)=0.95`

`P(A^(c)/GR)=(P(A^(c),GR))/(P(GR)) \\0.95=(P(A^(c),GR))/(0.2) \\P(A^(c),GR)=(0.95)(0.2) \\P(A^(c),GR)=0.19`

`P(GR/A^(c))=(P(GR,A^(c)))/(P(A^(c)))=(0.19)/(0.825)\\P(GR/A^(c))=0.2303`