Answer:
(1) No matter what's the value of
 ,
,
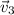 is never in the span of
is never in the span of
 and
and
 .
.
(2) The three vectors
 ,
,
 , and
, and
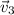 are always linearly dependent for all real
are always linearly dependent for all real
 .
.
Explanation:
(a)
If
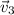 is in the span of
is in the span of
 and
and
 , there need to exist real
, there need to exist real
 and
and
 such that
such that
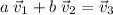 .
.
Assume that such
 and
and
 do exist.
do exist.
In other words,
![\displaystyle a \left[\begin{array}{c}{1 \\ -4\\2} \end{array}\right] + b\left[\begin{array}{c}{-4 \\ 16\\-8}\end{array}\right] = \left[\begin{array}{c}5 \\7 \\ h\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/jpf2dmlr21i2hq4xyiyrxmid4lefwv461a.png) .
.
![\displaystyle \left[\begin{array}{c}{a \\ -4a\\2a} \end{array}\right] + \left[\begin{array}{c}{-4b \\ 16b\\-8b}\end{array}\right] = \left[\begin{array}{c}5 \\7 \\ h\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/2gxmuqf0t9jwpsl9v8xc7kvkx9ufqee74i.png) .
.
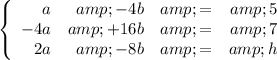 .
.
Rewrite as an augmented matrix and row-reduce:
![\displaystyle \left[ \begin{array}c 1 & -4 & 5 \\ -4 & 16 & 7 \\ 2 & -8 & h\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/n8by50qe3ubynip0i0x4qi55jjp9djap87.png) .
.
(Add four times row one to row two and
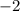 times row one to row three.)
times row one to row three.)
![\displaystyle \sim \left[ \begin{array}c 1 & -4 & 5 \\ 0 & 0 & 27 \\ 0 & 0 & h - 10\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/d4qfo5pqlc98x18kbcwfmn4cfy4gn1mym4.png) .
.
Note that in row two,
- Left-hand side:
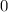 ;
; - Right-hand side:
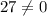 .
.
In other words, this system is inconsistent. There's no real
 and
and
 that would satisfy the condition
that would satisfy the condition
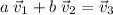 .
.
Hence
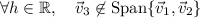 .
.
There's no real
 that allows
that allows
 ,
,
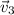 to be part of the span of
to be part of the span of
 and
and
 .
.
(b)
If the three vectors are linearly dependent, at least one of them can be expressed as the linear combination of the other two.
Note that
 . In other words,
. In other words,
 can be written as the linear combination of the other two vectors. Additionally, since the coefficient in front of
can be written as the linear combination of the other two vectors. Additionally, since the coefficient in front of
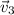 is zero, neither the exact value of
is zero, neither the exact value of
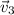 nor the value of
nor the value of
 will make a difference. Therefore, for all
will make a difference. Therefore, for all
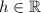 , the three vectors
, the three vectors
 ,
,
 , and
, and
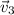 are linearly dependent.
are linearly dependent.