Answer:
E= 10.2 ev

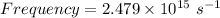
Step-by-step explanation:
It is given that energy in first exited state (n=2) ,
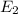 = -3.4 ev
= -3.4 ev
Also , it is given than energy in ground state (n=1) ,
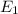 = -13.6 ev.
= -13.6 ev.
We know energy of photon released is difference of the final and initial level of electron.
Energy of photon released,
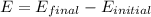
Therefore,
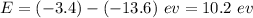 .
.
To convert energy from ev(electron volt) into joule we need to multiply energy in ev by charge of electron which is (
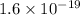 )
)
Therefore,
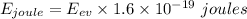
Now , we know that photon is an quantum of light . Therefore, speed of photon in vaccum is equal to speed of light which is ,
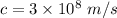 .
.
Now, by energy-wavelength relation,
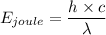
where ,
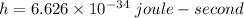
Now, putting values of h ,c and E in above equation .


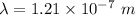
We know,

Therefore,
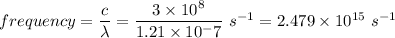
Hence, this is the required solution.