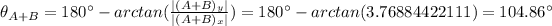Answer:
a)
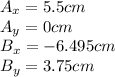
b)
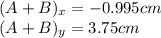
c)
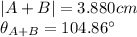
Explanation:
If we call A and B the longitude of the vectors, and measure
 from the positive x axis in anti-clockwise direction (as usual), the x and y components are determined by the formulas:
from the positive x axis in anti-clockwise direction (as usual), the x and y components are determined by the formulas:
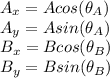
An angle of 30 degrees above the negative x axis is an angle of 180-30=150 degrees from the positive x axis in anti-clockwise direction. So we will have:

The sum of the 2 vectors (each of the components of their sum) in terms of their components will be:
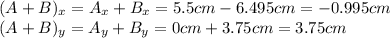
Since
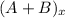 and
and
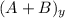 are the sides of a right triangle, the magnitude of the sum of A+B (which we will call |A+B|) will be given by the Pythagoras formula, and the angle can be calculated with the formula of the arc tangent since
are the sides of a right triangle, the magnitude of the sum of A+B (which we will call |A+B|) will be given by the Pythagoras formula, and the angle can be calculated with the formula of the arc tangent since
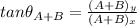 :
:
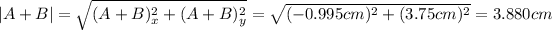
For the angle one has to be careful since the arctan function cannot interpret some results. In our case, the vector A+B is on Quadrant II (negative x, positive y), so the best way will be to calculate the angle above negative x (using the absolute values of the components), and to 180 substract this value, then: