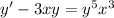
Divide both sides by
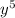 :
:
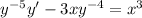
Substitute
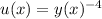 , so that
, so that
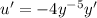 . Then we get a new ODE that is linear in
. Then we get a new ODE that is linear in
 ,
,
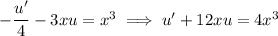
Multiply both sides by
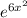 :
:
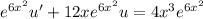
Notice that
 . Integrating both sides with respect to
. Integrating both sides with respect to
 gives
gives
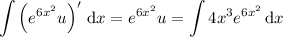

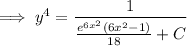
Given that
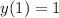 , we find
, we find
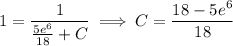
so the particular solution is
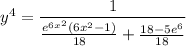
![\implies\boxed{y=\sqrt[4]{\frac1{(e^(6x^2)(6x^2-1))/(18)+(18-5e^6)/(18)}}}](https://img.qammunity.org/2020/formulas/mathematics/high-school/70fj08tjka1snyfv65zlk1ruhpeuvb9t5m.png)
where we take the positive root because the initial condition tells us to expect
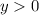 when
when
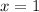 .
.