Answer with explanation:
Given : The heights of a certain population of corn plants follow a normal distribution with mean
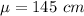 and standard deviation
and standard deviation
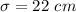
a) Using formula
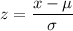 , the z-value corresponds to x= 135 will be
, the z-value corresponds to x= 135 will be
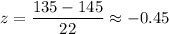
At x= 155,
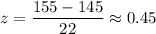
The probability that plants are between 135 and 155 cm tall :-
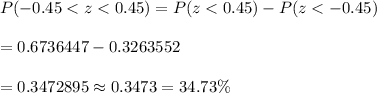
Hence, 34.73% of the plants are between 135 and 155 cm tall.
b) Sample size : n= 16
Using formula
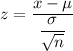 , the z-value corresponds to x= 135 will be
, the z-value corresponds to x= 135 will be
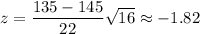
At x= 155,
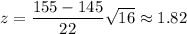
The probability that plants are between 135 and 155 cm tall :-
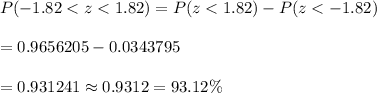
Hence,The percentage of the samples would the sample mean height be between 135 and 155 cm.= 93.12%