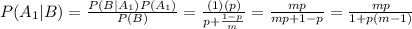Answer:
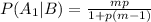
Explanation:
For mutually exclusive events as A1, A2, A3, etc, Bayes' theorem states:
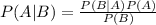
P(A|B) is a conditional probability: the likelihood of event A occurring given that B is true.
P(B|A) is a conditional probability: the likelihood of event B occurring given that A is true.
P(A) is the probability that A occurs
P(B) is the probability that B occurs
For this problem:
A1 is the probability that the student knows the answer
A2 is the probability that the student guesses the answer
B is the probability that the student answer correctly
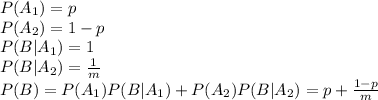
P(B|A₁) means the probability that the answer is correct when he knew the answer
P(B|A₂) means the probability that the answer is correct when he guessed the answer
P(A₁|B) means the probability that he knew the answer when the answer was correct
Replacing everything in the Bayes' theorem you get: