Answer:
16
Explanation:
We must find integers x, y with the most amount of prime divisors, not necessarily distinct, such that x + 3y < 1,000.
Obviously, this is achieved when the divisor is the least prime 2. So, we must find integers n, m such that

since
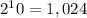 , then n must be 9. For n=9 we find the greatest integer m such that
, then n must be 9. For n=9 we find the greatest integer m such that
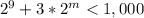
and we find m=7
and
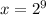 ,
,
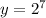 are the numbers we are looking for and the sum of their length is 9+7 = 16.
are the numbers we are looking for and the sum of their length is 9+7 = 16.
So, 16 is the maximum possible sum of the length of x and the length of y.