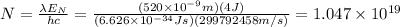Question

Recall from Chapter 1 that a watt is a unit of en- ergy per unit time, and one watt (W) is equal to one joule per second ( J·s–1). A 100-W incandescent light- bulb produces about 4% of its energy as visible light. Assuming that the light has an average wavelength of 510 nm, calculate how many such photons are emit- ted per second by a 100-W incandescent lightbulb.

Answer 1

Step-by-step explanation:

The energy of a photon is given by the equation
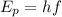`E_p=h f`, where h is the Planck constant and f the frequency of the photon. Thus, N photons of frequency f will give an energy of
`E_N=N h f`.

We also know that frequency and wavelength are related by
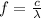`f=(c)/(\lambda)`, so we have
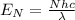`E_N=(N h c)/(\lambda)`, where c is the speed of light.

We will want the number of photons, so we can write

`N=(\lambda E_N)/(h c)`

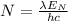
We need to know then how much energy do we have to calculate N. The equation of power is
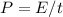`P=E/t`, so for the power we have and considering 1 second we can calculate the total energy, and then only consider the 4% of it which will produce light, or better said, the N photons, which means it will be
`E_N`.

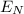Putting this paragraph in equations:

`E_N=((4)/(100))E=0.04Pt=(0.04)(100W)(1s)=4J`.

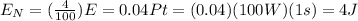And then we can substitute everything in our equation for number of photons, in S.I. and getting the values of constants from tables:

`N=(\lambda E_N)/(h c)=((520 *10^(-9)m) (4J))/((6.626*10^(-34)Js) (299792458m/s))=1.047 *10^(19)`