Question

A catapult launches a test rocket vertically upward from a well, giving the rocket an initial speed of 80.0 m/s at ground level. The engines then fire, and the rocket accelerates up- ward at 4.00 m/s2 until it reaches an altitude of 1 000 m. At that point, its engines fail and the rocket goes into free fall, with an acceleration of 29.80 m/s2. (a) For what time interval is the rocket in motion above the ground?

Answer 1

The time interval the rocket is in motion above the ground is the time in the two times the motion is going on
`T_(total) = 23,14 s`

Step-by-step explanation:

`V_(i) = 80 ((m)/(s) )`

`S_(i) = 0 m`

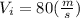
The motion in the first step has an acceleration
`a_(1) = 4 ((m)/(s^(2) ) )`

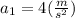
and the maximum height will be and the end of this step is
`S_(1) = 1000 m`

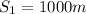
So to know the time until the rocket fail and change the acceleration:

`S_(1) = S_(i) + V_(i1)  * t + (1)/(2) * a_(1) *t^(2)`

`1000m = 0 m + 80 (m)/(s) * t + (1)/(2) * 4 (m)/(s^(2) )  * t^(2)`

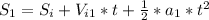
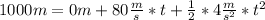
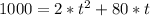`1000= 2*t^(2) + 80 * t` you can divide the expression by two and simplify the calculating

`2t^(2) + 80*t -1000=0`

`t^(2) + 40*t -500=0`

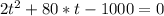
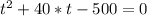
Using quadratic equation :

`\frac{-b +/- \sqrt{b^(2)-4*a*c } }{2*a}`

`\frac{- 40+/- \sqrt{40^(2)-4*-500 } }{2}`

`-20 +/-  30`

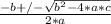
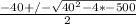
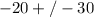
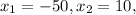`x_(1)= -50 , x_(2)= 10 ,` The time can be negative so, the time we are going to use is 10s

`t_(1)= 10 s`

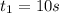
Now when the rocket fail it change the direction of the motion and the time is going to be the time it takes to reach earth again

`v_(f) = v_(i)+a_(1)*t_(1)`

`v_(f)= 80 (m)/(s) + 4 (m)/(s^(2) ) * 10 s = 120 (m)/(s)`

`S_(2) = S_(1) + V_(i2)  * t + (1)/(2) * a_(2)  *t^(2)`

`0m = 1000m + 120 (m)/(s) * t +(1)/(2) (-29,8 (m)/(s^(2) ))*t^(2)`

`0m = 1000m + 120 (m)/(s) * t -14,9 (m)/(s^(2) ))*t^(2)`

`\frac{-b +/- \sqrt{b^(2)-4*a*c } }{2*a}`

`\frac{- 120+/- \sqrt{120^(2)-4*-14,9*1000 } }{2*14,9}`

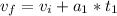
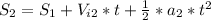
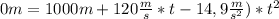
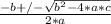
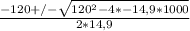
`x_(1)= -5,108s , x_(2)= 13,14 ,` The time can be negative so, the time we are going to use is 13,14s

So the full time is the both times adding them

`T_(total)= 10 + 13,14 = 23,14 s`