Question

A 112 g hockey puck sent sliding over ice is stopped in 16.8 m by the frictional force on it from the ice. (a) If its initial speed is 8.1 m/s, what is the magnitude of the frictional force? (b) What is the coefficient of friction between the puck and the ice?

Answer 1

Step-by-step explanation:

It is given that,

Mass of the hockey puck, m = 112 g = 0.112 kg

The hockey puck is stopped at a distance of 16.8 m.

(a) Initial speed of the puck, u = 8.1 m/s

We need to find the magnitude of the frictional force. Firstly, calculating the acceleration of the puck using third equation of kinematics as :

`v^2-u^2=2ax`

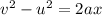
v = 0 (as it stops)

`-u^2=2ax`

`a=(-u^2)/(2x)`

`a=(-(8.1)^2)/(2* 16.8)`

`a=-1.95\ m/s^2`

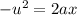
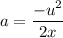
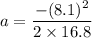
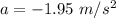
The frictional force is given by :

f = m a

`f=0.112\ kg* 1.95\ m/s^2`

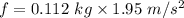
f = 0.218 N

(b) Also the frictional force is given by :

`f=\mu N`

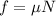
And N = mg (normal force)

`f=\mu mg`

`\mu=(f)/(mg)`

`\mu=(0.218)/(0.112* 9.8)`

`\mu=0.198`

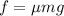
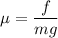
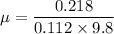
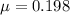
Hence, this is the required solution.