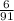Answer:
1.1296
2.570
3.
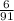
Explanation:
We are given that
Number of males=7 including George
Number of females=6 including Margaret
Number of children=4
Number of male selecting for roles=3
Number of females selecting for roles=1
Number of child selecting for roles=2
1.We have to find the number of ways can these roles be filled from these auditioners.
Total number of ways=
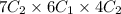
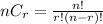
Using this formula
Total number of ways=
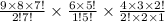
Total number of ways=1296
2.We have to find number of ways can these roles be filled if exactly one of George and Margaret gets a part.
If George gets a part then Margaret out
Total number of ways=
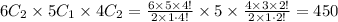
If Margaret gets a part then George out
Number of ways=
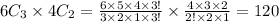
Therefore, total number of ways can these roles be filled if exactly one of George and Margaret gets a part=450+120=570
3.We have to find the probability of both George and Margaret getting a part.
Total number of audition=7+6+4=17
Except George and Margaret , number of auditions=15
Number of males=6
Probability=
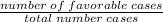
The probability of both George and Margaret getting a part=
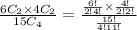
The probability of both George and Margaret getting a part=
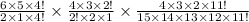
The probability of both George and Margaret getting a part=